今天來聊聊產生隨機排列與組合的方法。

先來個簡單版：若我們今天想要產生一個隨機排列，那麼我們可以考慮以下的 Fisher-Yates 演算法：假若一開始陣列中有 n 個元素，分別為 1 到 n。現在依序考慮每一個 i = 1, 2, …, n，我們隨機地將第 i 個位置的元素與任何一個 i~n 之間的元素交換。可以用數學歸納法證明，當我們做到第 i 個位置的時候，任何當前留在 i ~n 位置的元素被交換到第 i 個位置的機會均等。

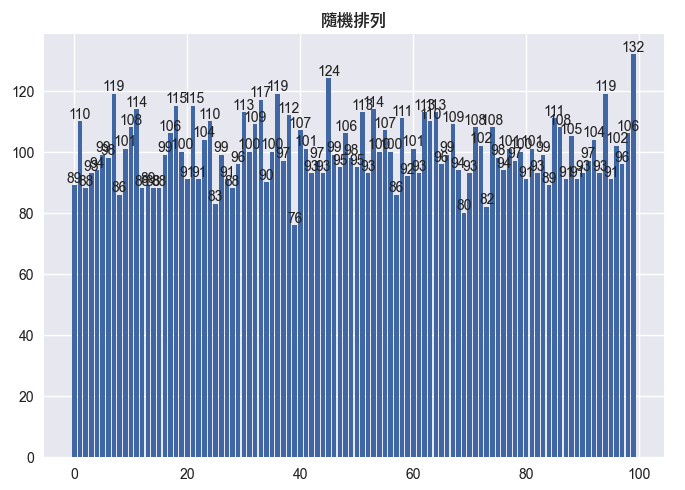
比方說，我們現在來實驗這個演算法，看看數字 k=1 出現在各個位置的分佈是否接近均勻。

# 一次實驗，回傳數字 k 出現的位置。
def simulate_shuffle(n, k):
    arr = [x for x in range(1, n+1)]
    for i in range(n):
        j = np.random.randint(i, n)  # 隨機選擇一個位置交換。
        arr[i], arr[j] = arr[j], arr[i]
    return arr.index(k)

        
rep = 10000  # 實驗次數
n = 100      # 陣列大小
k = 1        # 關心的數值
results = [simulate_shuffle(n, k) for _ in range(rep)]

# 把結果繪製出來
# plt.figure(figsize=(8, 1))
plt.bar(*np.unique(results, return_counts=True))
ax = plt.gca()
ax.bar_label(ax.containers[0], label_type='edge')
ax.set_title(f"隨機排列", fontname='LiHei Pro')
plt.show()

水塘抽樣是產生隨機組合的方法，其目的是要均勻地抓出水塘中隨意 k 個不同的數字形成的集合。它可以視為厲害版的非重複抽樣：所需要的記憶體其實只需要 O(k) 這麼多，這個對於串流式計算是相當有助益的。

方法如下：我們紀錄一個長度為 k 的陣列。然後對於索引為 i 的元素，我們決定一個 0~i 之間的隨機數，並且僅有在該數字介於 0 ~ k-1 之間的時候，將原陣列內容替換為 i 元素。如此一來，這些一個一個被考慮的資料就不一定要總是留在記憶體裡面了！

# 一次實驗，在 n 個數字中，選 k 個數字的集合。
def simulate_reservoir(n, k):
    arr = [i for i in range(k)]
    for val in range(k, n):
        i = np.random.randint(0, val+1)
        if i < k:
            arr[i] = val
    
    arr.sort()
    return str(arr)

        
rep = 100000  # 實驗次數
n = 10       # 陣列大小
k = 3        # 關心的數值
results = [simulate_reservoir(n, k) for _ in range(rep)]

# 把結果繪製出來
# plt.figure(figsize=(8, 1))
plt.bar(*np.unique(results, return_counts=True))
ax = plt.gca()
ax.bar_label(ax.containers[0], label_type='edge')
ax.set_title(f"隨機排列", fontname='LiHei Pro')
plt.show()

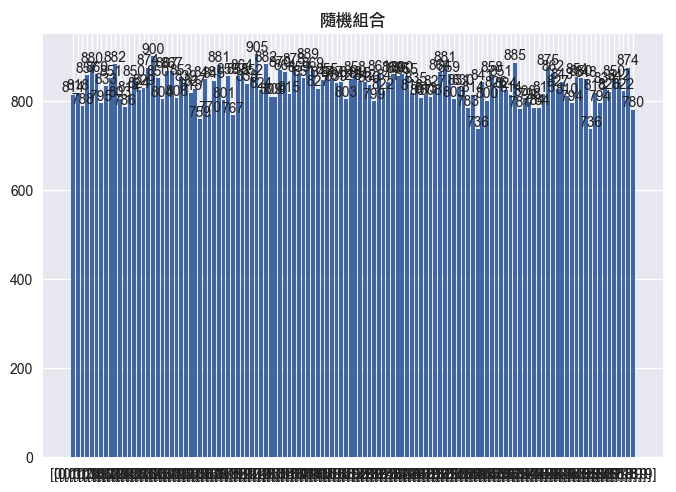
感覺今天的圖片們看起來都滿可怕的XD